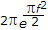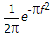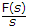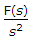IndiaBIX

Electronics and Communication Engineering - Signals and Systems

Exercise : Signals and Systems - Section 2
36.
F.T. of normalized Gaussian function e-pt2 is
e-pf2
2e-pt2
Answer: Option
Explanation:

Apply Differential Property of F.T

Note that this is true only for e-pt2

If g(t) = e-at2 then G(f) = .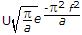

37.
If F(s) is the Laplace transform of f(t) then Laplace transform of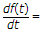
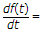
sFU(s)
s2F(s)
Answer: Option
Explanation:

£f(t) =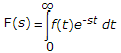

£-1F(s) = f(t)

£[a f1(t) + bf2(t)] = aF1(s) + bF2(s)

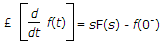
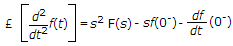
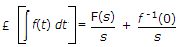
where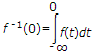

£[f(t - T)] = e-sT F(s)

£[e-at f(t)] = F(s + a)

Initial value theorem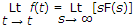

Final value theroem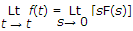

Convolution Integral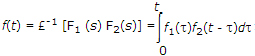

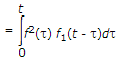
where t is dummy variable for t.

38.

Assertion (A): L[e-at f(t)] = F(s + a)

Reason (R): In use of Laplace transform method, initial conditions may be neglected.

Both A and R are correct and R is correct explanation of A
Both A and R are correct but R is not correct explanation of A
A is true, R is false
A is false, R is true
Answer: Option
Explanation:

Initial conditions are taken into account.

39.
An ac sinusoidal wave has an rms value of 10 V. The peak to peak value is
10 V
0 V
14.14 V
28.28 V
Answer: Option
Explanation:

Peak to peak value = 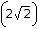(rms value).

40.
A complex wave is 5 + 5 sin ωt. Its rms value is
7.07 V
5 V
10 V
6.12 V
Answer: Option
Explanation:

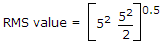
Quick links
Quantitative Aptitude
Verbal (English)
Reasoning
Programming
Interview
Placement Papers