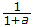IndiaBIX

Electronics and Communication Engineering - Signals and Systems

Exercise : Signals and Systems - Section 2
6.
If Laplace transform of f(t) is F(s), then £ f(t - a) u (t - a)= 0
eas F(s)
e-as F(s)
- eas F(s)
- e -as F(s)
Answer: Option
Explanation:

£f(t) =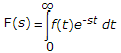

£-1F(s) = f(t)

£[a f1(t) + bf2(t)] = aF1(s) + bF2(s)

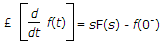
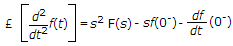
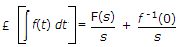
where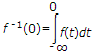

£[f(t - T)] = e-sT F(s)

£[e-at f(t)] = F(s + a)

Initial value theorem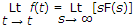

Final value theroem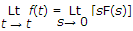

Convolution Integral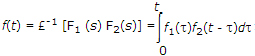

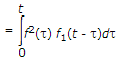
where t is dummy variable for t.

7.

Assertion (A): L[af1(t) + bf2(t)] = aF1(s) - bF2(s)

Reason (R): Initial value theroem enables us to find the value of f(t) at t = 0 directly from F(s)

Both A and R are correct and R is correct explanation of A
Both A and R are correct but R is not correct explanation of A
A is true, R is false
A is false, R is true
Answer: Option
Explanation:

£[af1(t) +bf2(t)] = aF1(s) + bF2(s) Hence A is wrong.

8.
The Laplace transform of impulse δ(t) is
1
1/s
s
1/s2
Answer: Option
Explanation:

£f(t) =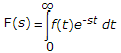

£-1F(s) = f(t)

£[a f1(t) + bf2(t)] = aF1(s) + bF2(s)

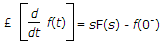
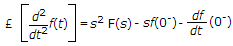
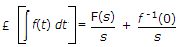
where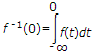

£[f(t - T)] = e-sT F(s)

£[e-at f(t)] = F(s + a)

Initial value theorem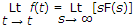

Final value theroem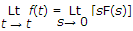

Convolution Integral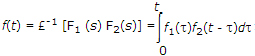

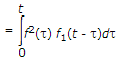
where t is dummy variable for t.

9.

Assertion (A): The modified ramp function of the given figure can be represented s sum of two ramp functions of the given figure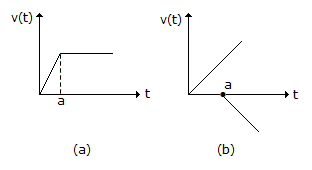

Reason (R): If f(t) = t, F(s) = 1

Both A and R are correct and R is correct explanation of A
Both A and R are correct but R is not correct explanation of A
A is true, R is false
A is false, R is true
Answer: Option
Explanation:

If f(t) = t, 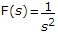Hence R is wrong.

10.
Energy density spectrum of x[n] = an∪[n] for -1 < a < + 1 is
Answer: Option
Explanation:

Quick links
Quantitative Aptitude
Verbal (English)
Reasoning
Programming
Interview
Placement Papers