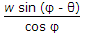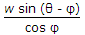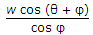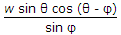IndiaBIX

Civil Engineering - Applied Mechanics

Exercise : Applied Mechanics - Section 4
36.
If a spherical body is symmetrical about its perpendicular axes, the moment of inertia of the body about an axis passing through its centre of gravity as given by Routh's rule is obtained by dividing the product of the mass and the sum of the squares of two semi-axes by n where n is
2
3
4
5.
Answer: Option
Explanation:
No answer description is available. Let's discuss.
37.
The angle of projection for a range is equal to the distance through which the particle would have fallen in order to acquire a velocity equal to the velocity of projection, will be
30°
45°
60°
75°.
Answer: Option
Explanation:
No answer description is available. Let's discuss.
38.
A particle executes a simple harmonic motion. While passing through the mean position, the particle possesses
maximum kinetic energy and minimum potential energy
maximum kinetic energy and maximum potential energy
minimum kinetic energy and maximum potential energy
minimum kinetic, energy and minimum potential energy
none of these.
Answer: Option
Explanation:
No answer description is available. Let's discuss.
39.
A body of weight w placed on an inclined plane is acted upon by a force P parallel to the plane which causes the body just to move up the plane. If the angle of inclination of the plane is θ and angle of friction is φ, the minimum value of P, is
Answer: Option
Explanation:
No answer description is available. Let's discuss.
40.
Varigon's theorem of moments states
arithmetical sum of the moments of two forces about any point, is equal to the moments of their resultant about that point
algebraic sum of the moments of two forces about any point, is equal to the moment of their resultant about that point
arithmetical sum of the moments of the forces about any point in their plane, is equal to the moment of their resultant about that point
algebraic sum of the moments of the forces about any point in their plane, is equal to the moment of their resulant about that point.
Answer: Option
Explanation:
No answer description is available. Let's discuss.
Quick links
Quantitative Aptitude
Verbal (English)
Reasoning
Programming
Interview
Placement Papers