Aptitude - Volume and Surface Area - Discussion
Discussion Forum : Volume and Surface Area - General Questions (Q.No. 1)
1.
A right triangle with sides 3 cm, 4 cm and 5 cm is rotated the side of 3 cm to form a cone. The volume of the cone so formed is:
12
cm3
cm315 cm3
cm316 cm3
cm320 cm3
cm3Answer: Option
Explanation:
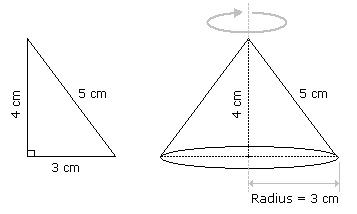
Clearly, we have r = 3 cm and h = 4 cm.
 Volume = |
1 | r2h = |
 |
1 | x x 32 x 4 |
 cm3 |
= 12 cm3. |
| 3 | 3 |
Video Explanation: https://youtu.be/Njsid2mVwUY
Discussion:
77 comments Page 8 of 8.
Prasad said:
6 years ago
How, h = 4? Explain me.
(1)
Pavithra said:
5 years ago
If it is rotated along 3 then won't it be height?
(2)
Saurav said:
5 years ago
It is not mentioned that the 3cm is the base. The triangle is rotated about an axis that becomes height after the rotation then the answer will be 16pie.
(7)
Tamil said:
5 years ago
If we rotate 3 cm we can form a cone with height 4 cm and hypotenuses 5cm as per Pythagoras theorem and apply the volume of cone 1/3πr^2h.
(2)
Rakshitha A. R said:
4 years ago
Please explain the answer.
(1)
Stragi said:
3 years ago
As the base is 3.
How can the radius will be 3?
Why can't it (3) be a perimeter which is equal to 2*3.14*r.?
And also if it is rotated as base 3 then 4, 5 lengths will be slant heights and (4, 5 are not equal and can't make a perfect cone also).
How can the radius will be 3?
Why can't it (3) be a perimeter which is equal to 2*3.14*r.?
And also if it is rotated as base 3 then 4, 5 lengths will be slant heights and (4, 5 are not equal and can't make a perfect cone also).
(5)
Bryan Roger said:
1 year ago
The BASE would be 4 and the HEIGHT would be 3. Because the side of 3cm is rotated, that is the height.
The final answer would be 16π cm^3 on solving using the formula 1/3 (π) (r^2) h.
The final answer would be 16π cm^3 on solving using the formula 1/3 (π) (r^2) h.
(2)
Post your comments here:
Quick links
Quantitative Aptitude
Verbal (English)
Reasoning
Programming
Interview
Placement Papers